
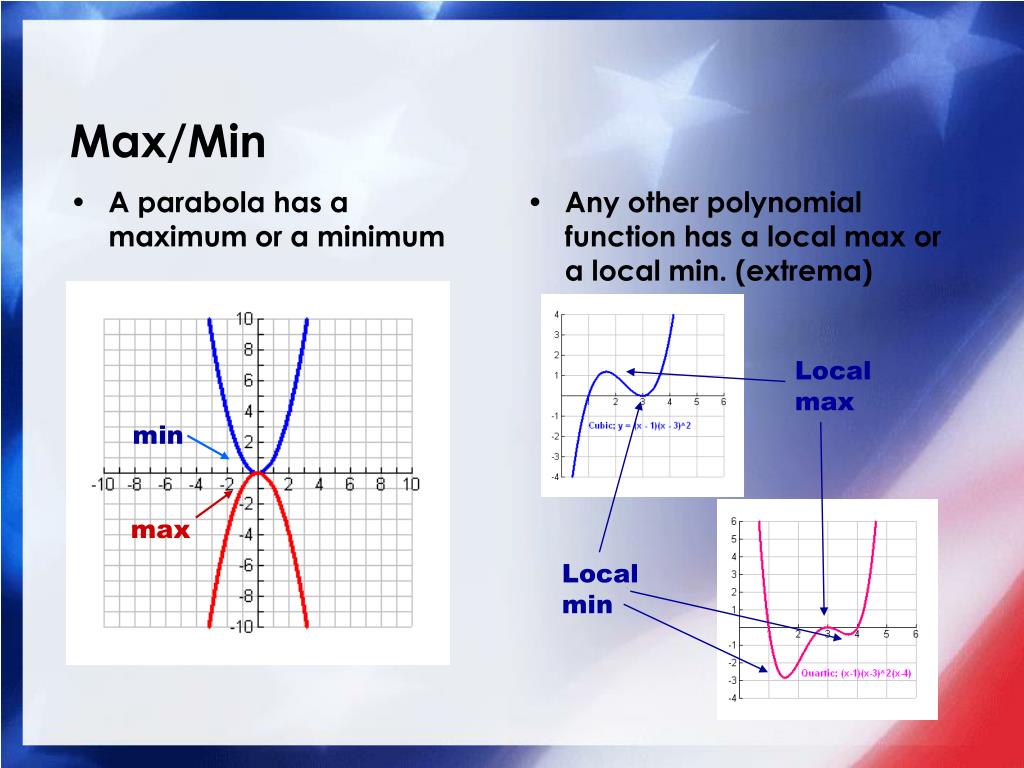
Will either ultimately rise or fall as x x + a 1 x + a 0 f ( x ) = a n x n + a n − 1 x n − 1 +. See Figure 8 for examples of graphs of polynomial functions with multiplicity 1, 2, and 3.į ( x ) = a n x n + a n − 1 x n − 1 +. For zeros with odd multiplicities, the graphs cross or intersect the x-axis. We call this a triple zero, or a zero with multiplicity 3.įor zeros with even multiplicities, the graphs touch or are tangent to the x-axis. This factor is cubic (degree 3), so the behavior near the intercept is like that of a cubic-with the same S-shape near the intercept as the toolkit function f ( x ) = x 3. The graph passes through the axis at the intercept, but flattens out a bit first. The x-intercept x = − 1 x = − 1 is the repeated solution of factor ( x + 1 ) 3 = 0. The zero associated with this factor, x = 2, x = 2, has multiplicity 2 because the factor ( x − 2 ) ( x − 2 ) occurs twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity.
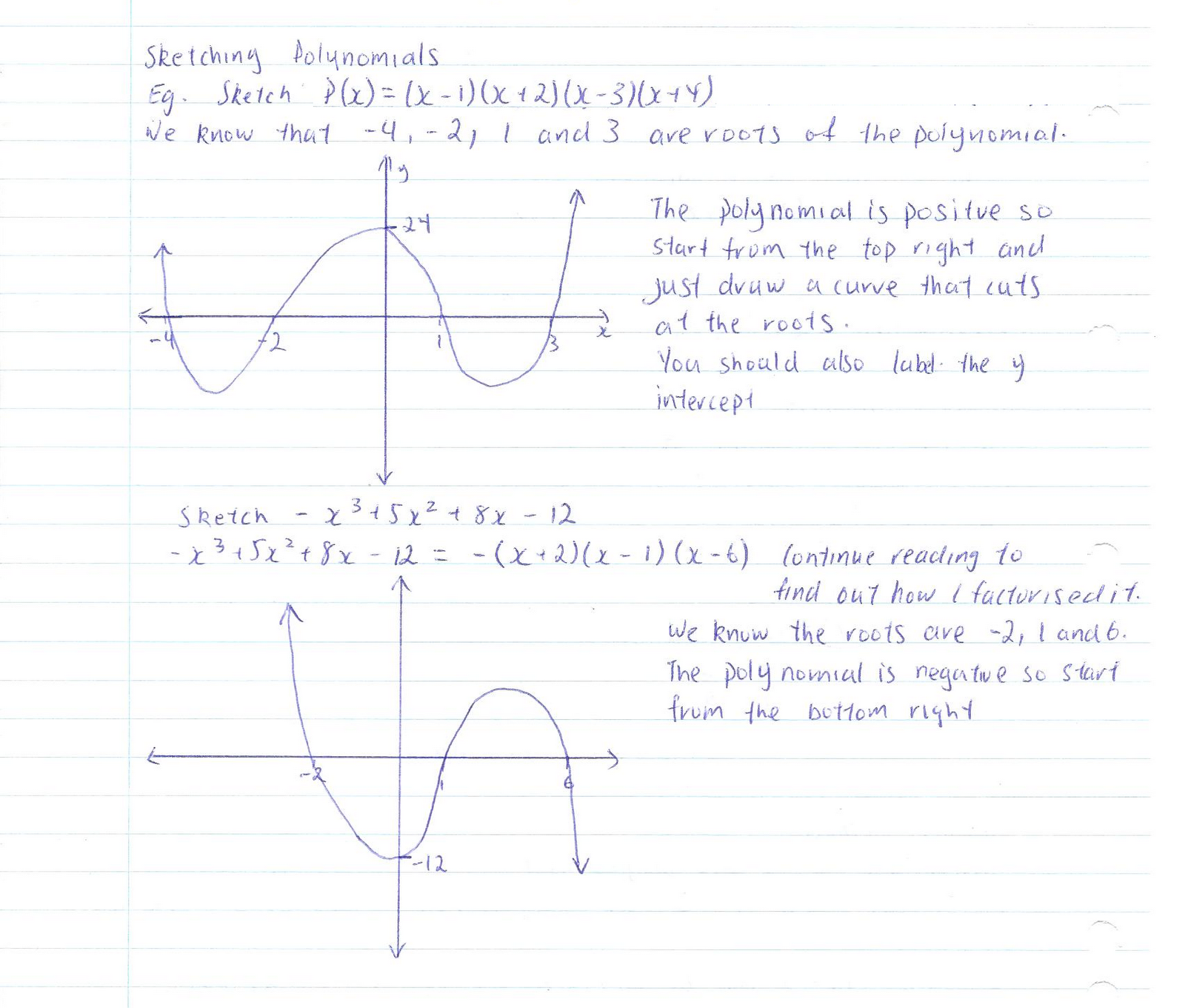
The factor is repeated, that is, the factor ( x − 2 ) ( x − 2 ) appears twice. Technology is used to determine the intercepts.The polynomial is given in factored form.The polynomial can be factored using known methods: greatest common factor and trinomial factoring.Consequently, we will limit ourselves to three cases: While quadratics can be solved using the relatively simple quadratic formula, the corresponding formulas for cubic and fourth-degree polynomials are not simple enough to remember, and formulas do not exist for general higher-degree polynomials. For general polynomials, this can be a challenging prospect. We can use this method to find x - x - intercepts because at the x - x - intercepts we find the input values when the output value is zero. If the equation of the polynomial function can be factored, we can set each factor equal to zero and solve for the zeros. Recall that if f f is a polynomial function, the values of x x for which f ( x ) = 0 f ( x ) = 0 are called zeros of f. Using Factoring to Find Zeros of Polynomial Functions Any real number is a valid input for a polynomial function. Figure 1 shows a graph that represents a polynomial function and a graph that represents a function that is not a polynomial.ĭo all polynomial functions have as their domain all real numbers? Curves with no breaks are called continuous. Polynomial functions also display graphs that have no breaks. Polynomial functions of degree 2 or more have graphs that do not have sharp corners recall that these types of graphs are called smooth curves. Recognizing Characteristics of Graphs of Polynomial Functions
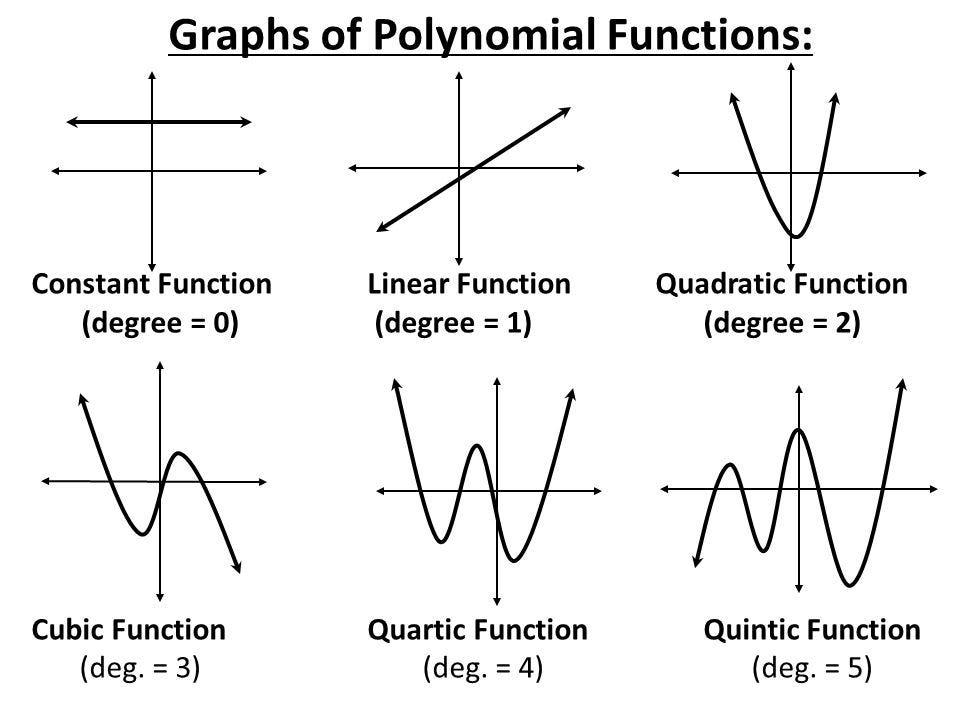
In this section we will explore the local behavior of polynomials in general. We have already explored the local behavior of quadratics, a special case of polynomials. Over which intervals is the revenue for the company increasing? Over which intervals is the revenue for the company decreasing? These questions, along with many others, can be answered by examining the graph of the polynomial function. Where R R represents the revenue in millions of dollars and t t represents the year, with t = 6 t = 6 corresponding to 2006.


 0 kommentar(er)
0 kommentar(er)
